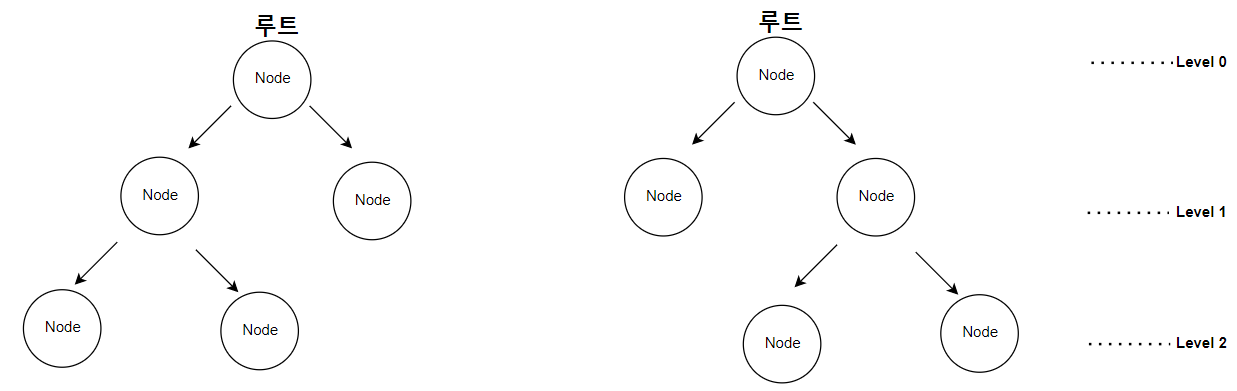
– 이진 트리란?
왼쪽/오른쪽 노드만 있는 트리를 이진 트리라고 합니다. 노드가 루트에서 하위 수준으로 가득 차고 노드가 왼쪽에서 오른쪽으로 마지막 수준으로 채워지는 이진 트리를 완전 이진 트리라고 합니다.
그러나 아래 그림과 같이 마지막 레벨의 시작 부분을 오른쪽에서 왼쪽으로 채우면 완전한 이진 트리가 아닙니다.
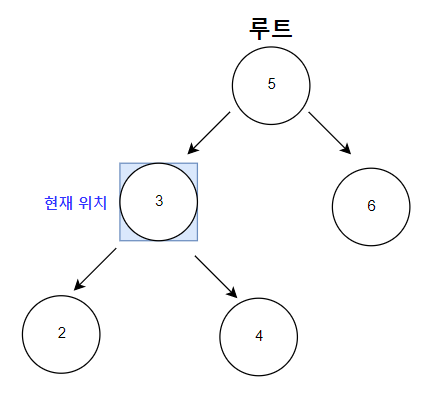
– 이진탐색트리란?
- 왼쪽 하위 트리 노드의 키 값은 자신 노드의 키 값보다 작고 오른쪽 하위 트리 노드의 키 값은 자신의 노드 키 값보다 큽니다.
위의 조건을 만족하면 이진 탐색 트리라고 합니다. 단순히 이미지로 표시하면 현재 위치에서 왼쪽이 작은 값이고 오른쪽이 큰 값임을 알 수 있습니다.
이진 검색 트리는 구조가 단순하여 DFS(깊이 우선 검색) 및 중위 순회를 통해 노드 값을 오름차순으로 빠르게 가져올 수 있습니다.
(참조)
- 순서 순회: 마지막 수준의 왼쪽에서 시작하여 왼쪽 자식 → 노드 → 오른쪽 자식 순회, e.g. 나.) 2 -> 3 -> 4 -> 5 -> 6
- DFS(깊이 우선 검색): 루트에서 리프에 도달할 때까지 검색하는 방법입니다.
– 이진 검색 트리 구현(Python)
class Node:
def __init__(self, key, value, left,right):
self.key = key
self.value = value
self.left = left
self.right = right
class BinarySearchTree: # 이진 검색 트리
def __init__(self):
self.root = None # 루트
# 키 값으로 값 찾기
def search(self,key):
p = self.root # root의 키 값
while True:
if p is None: # root 노드가 없으면 None을 출력
return None
if key == p.key: # 찾는 key 값이 현재 노드와 같으면 root의 값을 출력
return p.value
elif key < p.key: # 찾는 key 값이 현재 노드보다 작으면 왼쪽 하위 노드로 이동
p = p.left
else: # 찾는 key 값이 현재 노드보다 크면 오른쪽 하위 노드로 이동
p = p.right
# 값 추가하기
def add(self,key,value): # 해당 노드에 key와 값 추가
def add_node(node,key,value):
if key == node.key: # key가 이미 사용된 경우
return False
elif key < node.key: # 현재 키(node.key)보다 주어진 키가 작을 경우
if node.left is None: # 자식 노드가 없을 때 노드 연결
node.left = Node(key,value,None,None)
else: # 자식 노드가 있을 때 자식 노드로 이동
return add_node(node.left,key,value)
else: # 현재 키(node.key)보다 주어진 키가 클 경우
if node.right is None: # 자식 노드가 없을 때 노드 연결
node.right = Node(key,value,None,None)
else: # 자식 노드가 있을 때 자식 노드로 이동
return add_node(node.right,key,value)
if self.root is None: # root 노드가 없는 경우
self.root = Node(key,value,None,None)
return True
else: # root 노드가 있는 경우
return add_node(self.root, key,value)
# 값 삭제하기
def remove(self,key):
p = self.root # root 노드 저장
parent = None # 부모 노드 저장
is_left_child = True # 왼쪽 노드 존재 판단
while True:
if p is None: # 키가 존재하지 않는 경우
return False
if key == p.key: # key 와 p 노드의 키가 같으면 반복문 종료
break
else:
parent = p # 부모 노드 정보 저장
if key < p.key: # 키가 현재 노드보다 작다면
is_left_child = True # 왼쪽 자식
p = p.left
else: # 키가 현재 노드보다 크다면
is_left_child = False # 오른쪽 자식
p = p.right
if p.left is None: # 노드 하나 : p에 왼쪽 자식이 없으면
if p is self.root:
self.root = p.right
elif is_left_child:
parent.left = p.right
else:
parent.right = p.right
elif p.right is None: # 노드 하나 : p에 오른쪽 자식이 없으면
if p is self.root:
self.root = p.left
elif is_left_child:
parent.left = p.left # 부모의 왼쪽 포인터가 왼쪽 자식을 가리킵니다.
else:
parent.right = p.left # 부모의 오른쪽 포인터가 왼쪽 자식을 가리킵니다.
else: # 노드 두개 : p에 왼쪽과 오른쪽 자식이 있으면
parent = p
left = p.left # 서브 트리 안에서 가장 큰 노드
is_left_child = True
while left.right is not None: # 가장 큰 노드 left를 검색
parent = left
left = left.right
is_left_child = False
p.key = left.key # left의 키를 p로 이동
p.value = left.value # left의 데이터를 p로 이동
if is_left_child:
parent.left = left.left # left를 삭제
else:
parent.right = left.left # left를 삭제
return True
bst = BinarySearchTree()
bst.add(5,5)
bst.add(4,4)
bst.add(3,3)
print(bst.search(5)) # 출력 5
bst.remove(5)
print(bst.search(5)) # 출력 None